More on polarization of the vacuum and quantum field theory: electroweak symmetry and mass
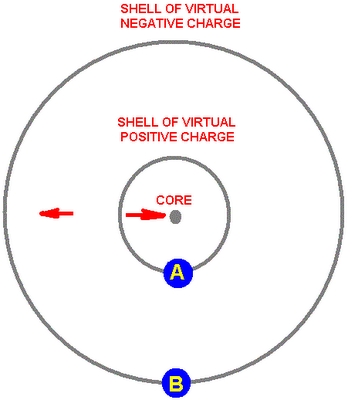
(Illustration above: by 'shell' I refer to the mean distance of the virtual positrons freed in the vacuum by the intense close in electric field, and the somewhat greater mean distance of the virtual electrons; obviously this is statistical and you not have every virtual electron at one radius and every virtual positron at another smaller radius from the real electron core.)
Quantum field theory implies the core of each real long-lived charge is surrounded by two concentric shells of charged vacuum particles: an inner shell with opposite charge to the core, and an outer one of similar charge to the core. The electric field arrow between the two shells points the other way to that for the charge from the core bare charge, so the latter is shielded. The shielding factor calculated in a previous post in this blog is approximately 137 or 1/alpha.
The physical reason why quarks have fractional charge can be explained very simply indeed. Electric charges are shielded by the polarized vacuum field they create at short distances. If you hypothetically put three electron charges close together so that they all share the same vacuum polarization cloud, the polarization in that cloud will be three times stronger. Hence, the shielding factor for electric charge will be three times greater. So the electric charge you would theoretically expect to get from each of the three electron-sized charges confined in close proximity is equal to: -1/3e. This is the electric charge of the downquark.
In the diagram above, the average distance of charged shells for any given species of vacuum loop charges is illustrated in a simple way. If the electron core couples to a particle in position A, then A will experience a charge 137 times stronger than a particle in position B. This is a simplified picture of the real situation (see recent posts on this blog for some issues with it).
However, it is mathematically correct if distance A corresponds to the upper collision energy cutoff corresponding to Standard Model fundamental force unification energy, and if distance B corresponds to the lower cutoff used in the quantum field theory.
Note that the electron core is not just a static electric charge but also has spin and a dipole magnetic field equal to 1 Bohr magneton in Dirac's quantum field theory. According to string theory, the core would be a closed string like an oscillating loop. However, string theory has no evidence and is not even wrong. If light contains oscillating positive to negative electric field energy, then you might split a gamma ray photon into two gravitationally trapped charges spinning around in small loops. Taking account of the Poynting vector for electromagnetic radiation, this predicts the spherically symmetrical radial electric field, dipole magnetic field, spin, mass and quantum field theory corrections to the dipole magnetic field of an electron.
In the diagram above, assume the real bare particle core can pair up with a transient virtual positron located in the shell position A. The increase in the magnetic moment which results for leptons is reduced by the 1/alpha or 137 factor due to shielding from the virtual positron's own polarization zone, and is also reduced by a factor of 2Pi because the two particles are aligned with opposite spins: the force gauge bosons being exchanged between them hit the spinning particles on the edges, which have a side-on length which is 2Pi times smaller than the full circumference of the particle. To give a real world example, it is well known that by merely spinning a missile about its axis you reduce the exposure of the skin of the missile to weapons by a factor of Pi. This is because the exposure is measured in energy deposit per unit area, and this exposed area is obviously decreased by a factor of Pi if the missile is spinning quickly. For an electron, the spin is half integer, so like a Mobius strip (paper loop with half a turn), you have to rotate 720 degrees (not 360) to complete a 'rotation' back to the starting point. Therefore the effective exposure reduction for a spinning electron is 2Pi, rather than Pi.
Hence by combining the polarization shielding factor with the spin coupling factor, we can account for the fact that the lepton magnetic moment increase due to this effect is approximately 1/(2.Pi x 137) = alpha/(2.Pi) added on to the 1 Bohr magneton of the bare real electron. This gives the 1.0116 Bohr magnetons result for leptons.
The Z boson of electroweak theory is unique because it has rest mass despite being an uncharged fundamental particle! You can easily see how charged particles acquire mass (by attracting a cloud of vacuum charges, which mire them, creating inertia and a response to the spacetime fabric background field which is gravity). But how does a non-composite neutral particle, the Z, acquire mass? This is essentially the question of electroweak symmetry breaking at low energy. The Z is related to the photon, but is different in that it has rest mass and therefore has a limited range, at least below electroweak symmetry breaking energy.
Z mass model: a vacuum particle with the mass of the electroweak neutral gauge boson (Z) semi-empirically predicts all the masses in the Standard Model. You use data for a few particles to formulate the model, but then it predicts everything else, including making many extra checkable predictions! Here's how. If the particle is at position A in the model above, it is inside the polarization range of the electron, but there is still its own polarization shell separating it from the real electron core. Because of the shielding of its own shell of vacuum polarization and from the spin of the electron core, the mass it gives the core is equal to Mz/(2.Pi x 137) =
Mzalpha/(2.Pi) ~ 105.7 MeV. Hence the muon!
Next, consider the lower energy state where the mass is at position B in the diagram above. In that case, the coupling between the central core charge and the mass at B is reduced by the additional distance (which empirically is a factor of ~1.5 reduction) and also the 137 or 1/alpha polarization attenuation factor. Hence
Mz(alpha)2/(1.5 x 2.Pi) ~ 0.51 MeV. Hence the electron!
Generalizing, for n real charge cores (such as a bare lepton or 2-3 bare quarks), and N masses of Z boson mass at position A (a high energy, high mass state), the formula for predicting the observable mass of the elementary particle is: Men(N+1)/(2.alpha)
= Mzn(N+1)(alpha)/(6.Pi).
This does make predictions! It is based on known facts of polarization in the vacuum, the details of which have evidence from many experiments. It has more physics and checkable tests going for it than the periodic table of chemistry had first proposed from sheer empirical association by Newlands and Mendeleev, which today would doubtless be suppressed sneeringly as 'numerology' (the reason for the periodic table had to await the discovery of quantum mechanics). It produces a kind of periodic table of elementary particle masses which are directly comparable to measured data. This fact-guided methodology of doing physics is in stark contrast to stringy, abject, useless extra dimensional speculation.
The stringy model doesn't predict the force mechanisms, strengths, particle masses, and cosmological results which it suppressed with censorship.
But for a comparison of the above heuristic ideas with those quantum field theory between the Tomonaga-Feynman-Schwinger quantum field theory renormalized calculation of the magnetic field increase for an electron due to the vacuum (which Dirac and Feynman, as well as others like Dr Chris Oakley, raise objects to on mathematical grounds, as being incomplete/fiddled) see:
Julian Schwinger, On Gauge Invariance and Vacuum Polarization, Phys. Rev. vo. 82 (1951), p. 664:
'This paper is based on the elementary remark that the extraction of gauge invariant results from a formally gauge invariant theory is ensured if one employs methods of solution that involve only gauge covariant quantities. We illustrate this statement in connection with the problem of vacuum polarization by a prescribed electromagnetic field. The vacuum current of a charged Dirac field, which can be expressed in terms of the Green's function of that field, implies an addition to the action integral of the electromagnetic field. Now these quantities can be related to the dynamical properties of a "particle" with space-time coordinates that depend upon a proper-time parameter. The proper-time equations of motion involve only electromagnetic field strengths, and provide a suitable gauge invariant basis for treating problems. Rigorous solutions of the equations of motion can be obtained for a constant field, and for a plane wave field. A renormalization of field strength and charge, applied to the modified lagrange function for constant fields, yields a finite, gauge invariant result which implies nonlinear properties for the electromagnetic field in the vacuum. The contribution of a zero spin charged field is also stated. After the same field strength renormalization, the modified physical quantities describing a plane wave in the vacuum reduce to just those of the maxwell field; there are no nonlinear phenomena for a single plane wave, of arbitrary strength and spectral composition. The results obtained for constant (that is, slowly varying fields), are then applied to treat the two-photon disintegration of a spin zero neutral meson arising from the polarization of the proton vacuum. We obtain approximate, gauge invariant expressions for the effective interaction between the meson and the electromagnetic field, in which the nuclear coupling may be scalar, pseudoscalar, or pseudovector in nature. The direct verification of equivalence between the pseudoscalar and pseudovector interactions only requires a proper statement of the limiting processes involved. For arbitrarily varying fields, perturbation methods can be applied to the equations of motion, as discussed in Appendix A, or one can employ an expansion in powers of the potential vector. The latter automatically yields gauge invariant results, provided only that the proper-time integration is reserved to the last. This indicates that the significant aspect of the proper-time method is its isolation of divergences in integrals with respect to the proper-time parameter, which is independent of the coordinate system and of the gauge. The connection between the proper-time method and the technique of "invariant regularization" is discussed. Incidentally, the probability of actual pair creation is obtained from the imaginary part of the electromagnetic field action integral. Finally, as an application of the Green's function for a constant field, we construct the mass operator of an electron in a weak, homogeneous external field, and derive the additional spin magnetic moment of α/2π magnetons by means of a perturbation calculation in which proper-mass plays the customary role of energy.'


5 Comments:
Copy of a comment in case deleted
http://christinedantas.blogspot.com/2006/06/some-announcements.html
nigel said...
Dear Anonymous,
Some consider Popper a charlatan. For example Imre Lakatos:
‘Scientists have thick skins. They do not abandon a theory merely because facts contradict it. ... History of science, of course, is full of accounts of how crucial experiments allegedly killed theories. But such accounts are fabricated long after the theory had been abandoned. ... What really count are dramatic, unexpected, stunning predictions: a few of them are enough to tilt the balance; where theory lags behind the facts, we are dealing with miserable degenerating research programmes. Now, how do scientific revolutions come about? If we have two rival research programmes, and one is progressing while the other is degenerating, scientists tend to join the progressive programme. This is the rationale of scientific revolutions. ... Criticism is not a Popperian quick kill, by refutation. Important criticism is always constructive: there is no refutation without a better theory. Kuhn is wrong in thinking that scientific revolutions are sudden, irrational changes in vision. The history of science refutes both Popper and Kuhn: on close inspection both Popperian crucial experiments and Kuhnian revolutions turn out to be myths: what normally happens is that progressive research programmes replace degenerating ones.’ – Imre Lakatos, Science and Pseudo-Science, pages 96-102 of Godfrey Vesey (editor), Philosophy in the Open, Open University Press, Milton Keynes, 1974.
Read Popper's silly book. He totally ignores Archimedes' proofs of the laws of buoyancy (On Floating Bodies, Books 1 and 2).
You really ought to see how Archimedes PROVES things using EXPERIMENTAL FACTS + LOGIC.
Popper's claim about science having to be potentially "falsifiable" is totally inconsistent with Archimedes' proofs of physical laws.
Hence Popper is plain wrong.
All Popper has done in Logic of Scientific Discovery, 1934, is to describe one mythical approach to science, which is allegedly taken by modern physics (although the detailed history of modern physics shows it is all - apart from stringy stuff - empirically based):
Anyone who formulates a law EMPIRICALLY, i.e., from plotting good carefully checked experimental data and finding a formula to fit the curves, is not doing what Popper describes, because that isn't falsifiable.
Even Einstein's special relativity was not falsifiable when you realise that it is based on empirical facts,
(1) both at the input end (i.e., invariance of light speed and electromagnetism implied by Maxwell's EMPIRICALLY based laws - which summarise Coulomb/Gauss' law, Faraday's law of induction, and Ampere's law, all of which are basically EXPERIMENTAL FACTS), and
(2) at the output end (i.e., all of Einstein's special relativity results were already in existence under the names of FitzGerald 1889, Lorentz 1893, Larmor 1901, Poincare 1904, etc.).
The same goes for quantum mechanics, which was mathematicals developed to explain empirical data on atomic structure, spectral line splitting (spin), etc.
There is no substance in Popper's philosophy (although his claim that Heisenberg's uncertainty principle is a vacuum particle scattering formula is very valuable, he doesn't give full proofs of causality being behind quantum mechanics).
Read the letter Popper reproduces from Einstein in the book. Popper wrote to Einstein claiming that statistical uncertainty cannot emerge from a deterministic theory.
Einstein responded with a brilliant letter showing that if you have a material point moving in a simple circle at uniform speed, and you do not know its initial state, you can only describe the material point by statistics. Hence, you can easily calculate the probability of locating it on any length of the perimeter of the circle at a given time. Popper was wrong on many of his forcefully argued claims. Perhaps if he had checked them first, he would have save some people a lot of silliness.
Best wishes!
6/13/2006 04:40:56 PM
Copy of a comment:
http://meopemuk2.blogspot.com/2006/07/how-we-can-improve-qft.html
nigel said...
Improve it by finding a full causal dynamics representation for the best verified quantum field theory, the Yang-Mills Standard Model!
For example, the exchange radiation causing forces should be quantified and represented by a dynamic model.
The physical reasons for the renormalization cutoffs required should be explained in causal terms by a model which can then itself be checked via making predictions that can be tested.
The key thing about renormalization is that the polarized vacuum around a particle cancels out most of the core charge, but not all of it.
Why doesn't the vacuum polarize enough to completely cancel out charges?
I don't think the creation-annihilation operators are clearly understood in quantum field theory.
What seems to be the case is that the strong field near a charge actually cause the virtual vacuum charges, as well as polarizing them. Because of the way the abundance of virtual charges in the vacuum falls off with distance from the real charge core, there is a limit to the amount of cancelation by polarization, so some charge continues to be seen even at long distances.
This is different from Dirac's sea, in which the entire vacuum is full of virtual charge.
So I think renormalized QFT indicates that the virtual charges of the vacuum are confined very close to the real charges, and don't extend everywhere.
This brings up the electroweak symmetry breaking problem. As I understand it, at low energy the vacuum attenuates 3 out of the 4 electroweak gauge bosons, by giving them mass (W+, Z-, Zo).
The mass breaks the symmetry, since the photon is a massless version of the Zo. This indicates that the Zo is a very important particle to study, being the massive partner of the photon.
Above electroweak unification energy, the mass causing agent (Higgs field?) dissociates from the electroweak gauge bosons, so symmetry is restored and all the gauge bosons then have infinite range.
Physically what this means is that, at high energy, things interact with a massive energy compared to the binding energy between charges and masses (Higgs particles or whatever).
Hence, the masses cease to dominate the electroweak charged gauge bosons.
Again, this raises the question what happens to the neutral but massive gauge boson Zo?
That is the key to everything. Why does it have mass?
If you look at its mass, it is very interesting. Multiply Zo mass by alpha/(2Pi), and you get 105.7 MeV, the muon mass.
Multiply Zo mass by (alpha)^2 /(2Pi) and you get 0.51 MeV, electron mass.
Finally, multiply Zo mass by n(N+1)(alpha)/(6Pi), where n is the number of real charges in close proximity (sharing the same electroweak polarized vacuum veil, eg n = 1 for leptons, n = 3 quarks for nucleons) and N is an integer.
This formula predicts quantized masses of all particles! You can test statistically and find that the data fits this formula well.
For the QFT physical mechanism behind these formula see:
http://electrogravity.blogspot.com/2006/06/more-on-polarization-of-vacuum-and.html
5:55 AM
9 July 06
NOTE ABOUT SCHEMATIC ILLUSTRATION AT TOP OF PAGE: by "shell" I refer to the mean distance of the virtual positrons freed in the vacuum by the intense close in electric field, and the somewhat greater mean distance of the virtual electrons; obviously this is statistical and you will not have every virtual electron at one radius and every virtual positron at another smaller radius from the real electron core.
RADIUS OF OUTER SHELL IS ON THE ORDER OF 10^-15 METERS:
FREEMAN DYSON'S 1951 QED LECTURES
Woit reports that Dyson’s lectures on QED are online at http://arxiv.org/abs/quant-ph/0608140 which on page 70 states:
‘Because of the possibility of exciting the vacuum by creating a positron-electron pair, the vacuum behaves like a dielectric, just as a solid has dielectric properties in virtue of the possibility of its atoms being excited to excited states by Maxwell radiation. This effect does not depend on the quantizing of the Maxwell field, so we calculate it using classical fields.
‘Like a real solid dielectric, the vacuum is both non-linear and dispersive, i.e. the dielectric constant depends on the field intensity and on the frequency. And for sufficiently high frequencies and field intensities it has a complex dielectric constant, meaning it can absorb energy from the Maxwell field by real creation of pairs.’
Pairs are created by the high intensity field near the bare core of the electron, and the pairs become polarised, shielding part of the bare charge. The lower limit cutoff in the renormalized charge formula is therefore due to the fact that polarization is only possible where the field is intense enough to create virtual charges.
This threshold field strength for this effect to occur is 6.9 x 10^20 volts/metre. This is the electric field strength by Gauss’ law at a distance 1.4 x 10^-15 metre from an electron, which is the maximum range of QED vacuum polarization. This distance comes from the ~1 MeV collision energy used as a lower cutoff in the renormalized charge formula, because in a direct (head on) collision all of this energy is converted into electrostatic potential energy by the Coulomb repulsion at that distance: to do this just put 1 MeV equal to potential energy (electron charge)^2 / (4Pi.Permittivity.Distance).
Can someone explain to me why there are no books or articles with plots of observable (renormalized) electric charge versus distance from a quark or lepton, let alone plots of weak and nuclear force as a function of distance? Everyone plots forces as a function of collision energy only, which is obfuscating. What you need is to know is how the various types of charge vary as a function of distance. Higher energy only means smaller distance. It is pretty clear that when you plot charge as a function of distance, you start thinking about how energy is being shielded by the polarized vacuum and electroweak symmetry breaking becomes clearer. The electroweak symmetry exists close to the bare charge but it breaks at great distances due to some kind of vacuum polarization/shielding effect. Weak gauge bosons get completely attenuated at great distances, but electromagnetism is only partly shielded.
31 Aug 2006.
To convert energy into distance from particle core, all you have to do is to set the kinetic energy equal to the potential energy, (electron charge)^2 / (4Pi.Permittivity.Distance). However, you have to remember to use the observable charge for the electron charge in this formula to get correct results (hence at 92 GeV, the observable electric charge of the electron to use is 1.07 times the textbook low-energy electronic charge).
Post a Comment
<< Home